Introduction
Sequential Quantum Gate Decomposer (SQUANDER) package provides an interface to Python which makes it possible to combine SQUANDER with well known quantum computing back ends, like Qiskit. In fact, SQUANDER has already established an interface to export the decomposed quantum circuit in Qiskit format. The Python interface of SQUANDER is developed C++ extensions, while all the massive calculations related to the decomposition run in C++, and only the input and final output parameters are casted between C++ and Python types.
In the forthcoming sections we provide some tricks and best practices to use the SQUANDER Python interface. The SQUANDER Python interface can be tested by running the test cases by pytest utility or by example scripts in the examples directory of the source directory of the SQUANDER package: (To build the SQUANDER package follow the manual at Main Page.)
or
The script example.py solves two problems:
- the decomposition of a general three-qubit unitary
- the decomposition of the 4th IBM Challenge problem
The expected outcome of the test script should look as:
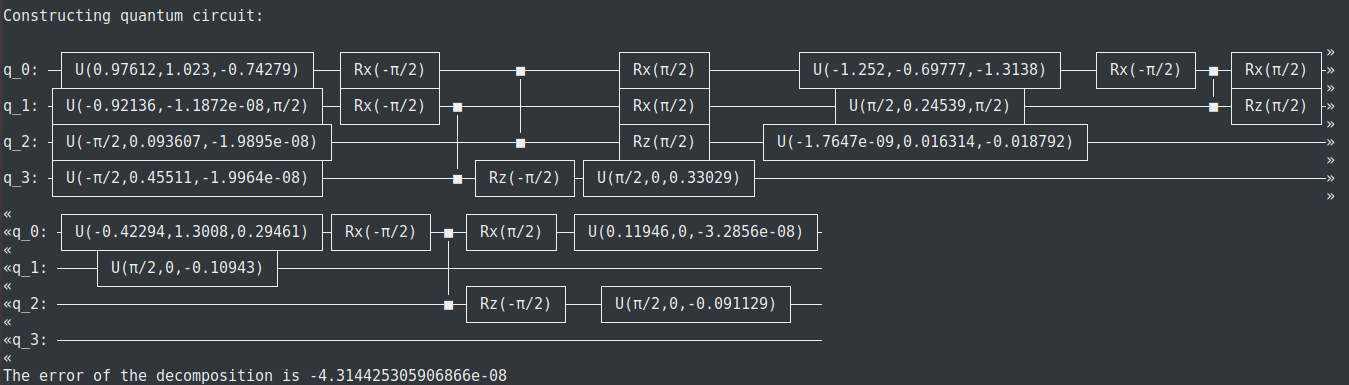
The output informs us that the 4th IBM Challenge problem was solved by using 4 CNOT gates with decomposition error \(4.31\times10^{-8}\). It is evident that the given decomposition can be further simplified by the union of successive U3 operations, however the SQUANDER package is not equipped yet to do such simplifications. (The decomposition result of the general three-qubit matrix can be found above the result of the IBM challenge on the standard output.)
Writing your own scripts
In this example we show how to use the python interface of the SQUANDER package for our own purposes. To this end we demonstrate the steps provided in the examples test_QX2.py and example.py to decompose a 4-qubit unitary onto the QX2 architecture of IBM, and to solve the 4th problem of the IBM Challenge 2020, respectively.
Decomposing general unitary for QX2 architecture
The ability to decompose a quantum program into gate structures with sparse connectivity is undoubtedly an important issue of quantum programming. One theoretically possible way to overcome this issue is to apply swap gates to get distant qubits close to each other where the desire two-qubit controlled operation can be applied on them, and then move the qubits back to their initial position by another swap operations. Here we report on a novel approach to optimize a quantum circuit of general unitaries. The key point of our approach is to find the best decomposition of a quantum program from the start, without implementing additional swap gates into the decomposed circuit.
The QX2 architecture consists of 5 qubits. In order to decompose a 4-qubit unitary on this system we need to select four qubits from the five.
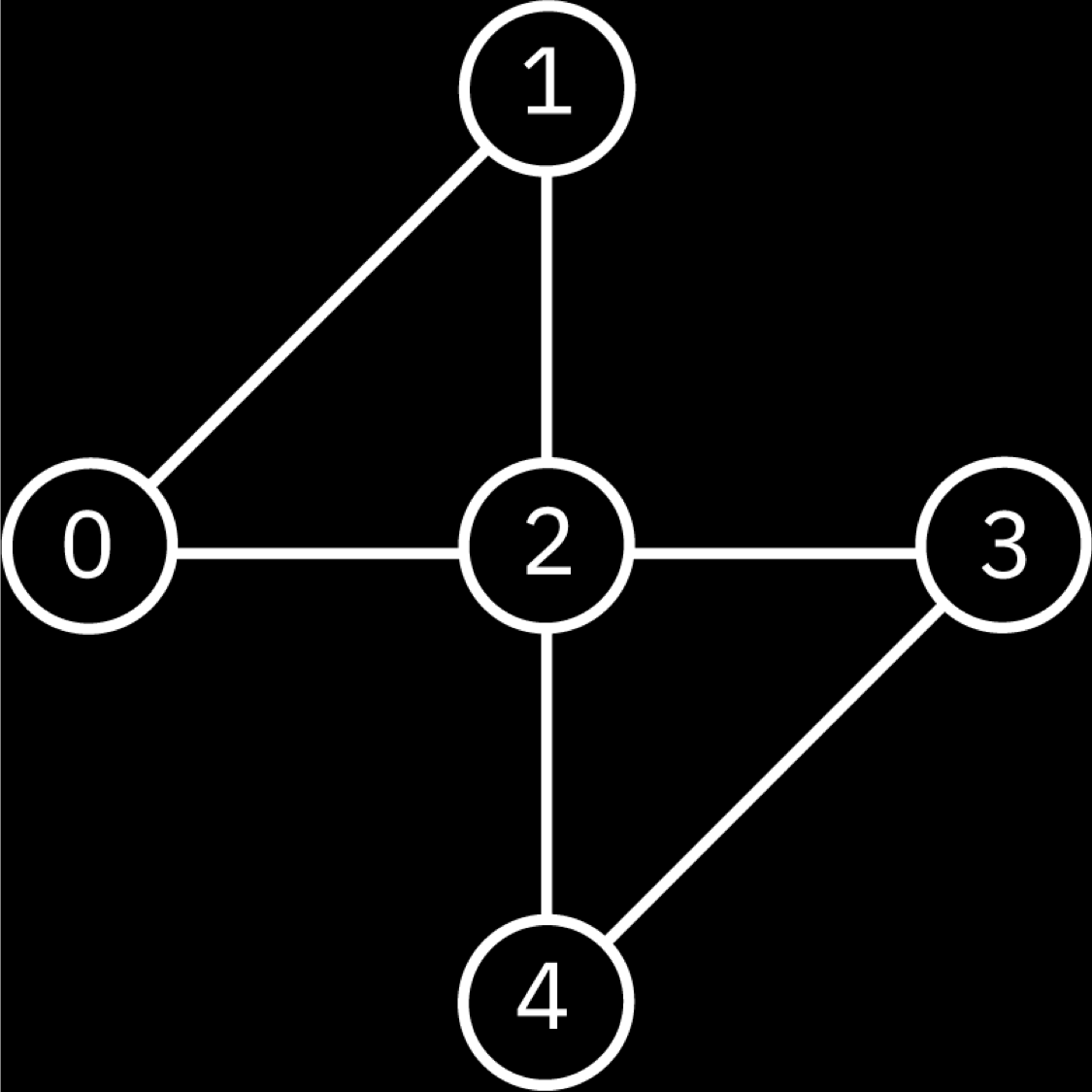
The choice of the four qubits might be in principle arbitrary, as long as the chosen set contains the central q2 qubit. In our example we decompose a general 4-qubit unitary on qubits q0, q1, q2 and q3 of the QX2. At the beginning of the decomposition we need to decide the order in which we are going to disentangle the qubits from the others. In general, qubits having the most connections are the easiest to disentangle from the others. However, since qubit q2 plays a central role in the design, we need to choose another qubit to begin with, otherwise there would be left no direct connection to qubit q3 and it would be not possible to finish the decomposition without using swap gates. For example, we might choose qubit q0 as the first one to disentangle. (We notice that at this point qubit Q1 would be equivalently good choice.) Then we can continue the decomposition with getting qubit q1 independent from the others, and finally we disentangle the remaining two qubits q2 and q3.
Now we proceed by the description of the specific programming steps of the above described desomposition strategy. The SQUANDER Python interface is installed into the Python module qgd_python located in the installation path of the SQUANDER package. In order to start using the SQUANDER Python interface, one need to import the python binding for the N_Qubit_Decomposition class:
In general, to import the SQUANDER Python module the Python interpreter should see it on the module search path (for further details see the module tutorial). In the next step we define the number of the qubits for which a random unitary is constructed.
Now we create a random unitary to be decomposed:
After successful import of the qgd_python.decomposition.qgd_N_Qubit_Decomposition class we create an instance of class used to bring the given unitary into identity by a sequence of two-qubit and one-qubit gates:
Notice, that we gave the complex transpose of the unitary Umtx as an input for the class qgd_python.decomposition.qgd_N_Qubit_Decomposition. This can be explained by simple linear algebra considerations: since the product of the unitary with it's complex transpose ( \(U U^\dagger=I\)) gives identity, the sequence of operations bringing a unitary \(U\) into identity would naturally equal to the complex transpose \(U^\dagger\) of the unitary \(U\).
Since the SQUANDER package process the decomposition of general unitaries in specific order of the qubits (always disentangling the qubit with the highest index), we need to re-label the qubits, so SQUANDER can disentangle the qubits in the correct order by instructions:
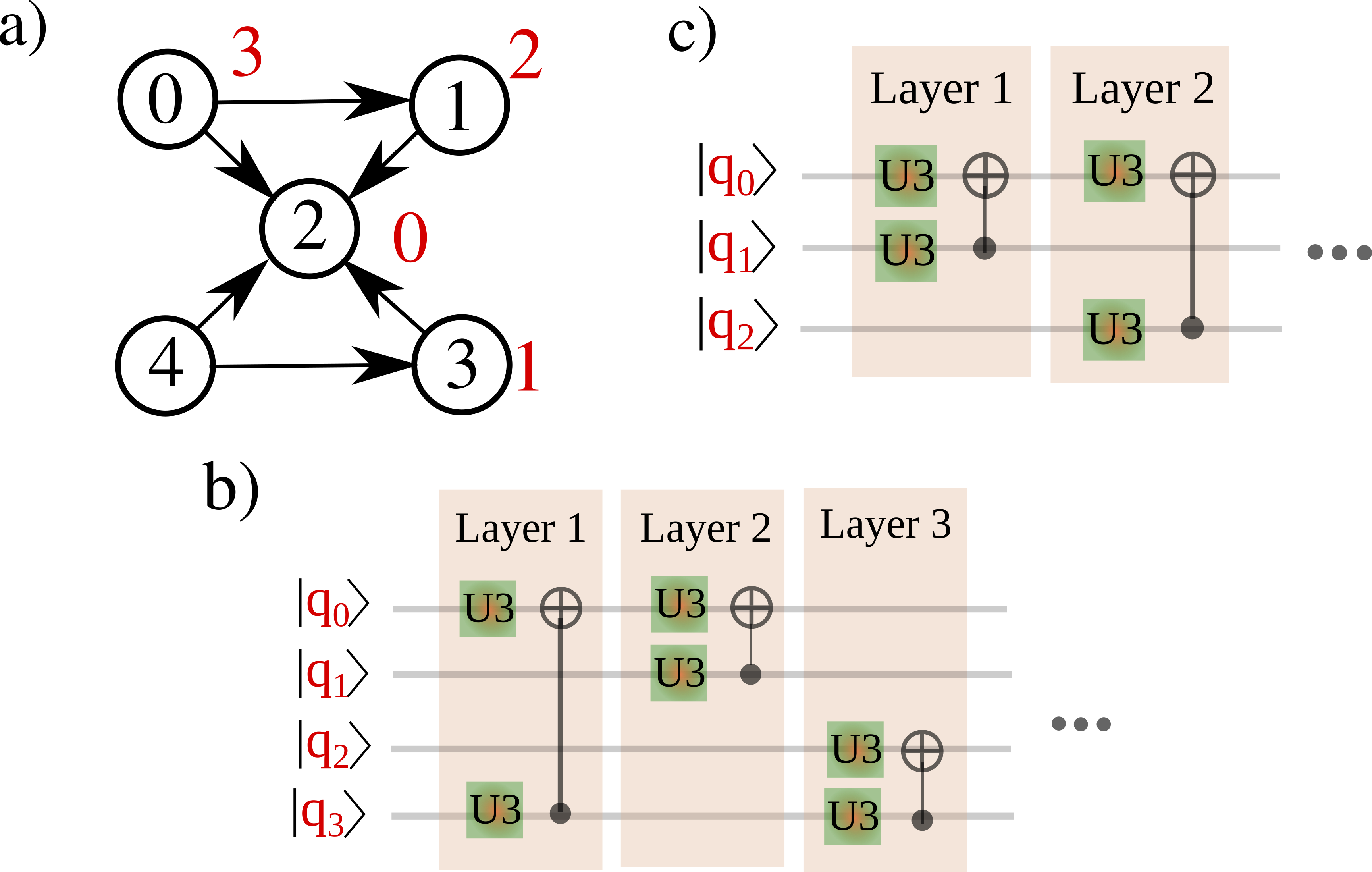
The relabeled qubits are indicated by the red numbers in the figure above showing the "Decomposing gate structure for the QX2 architecture". After relabeling the qubits, we set the custom gate structure by:
The python dict gate_structures contains a period of decomposing gate structures to disentangle the 4-th and the 3-rd qubit. These gate structure segments are created with an individual function create_custom_gate_structure_QX2 described in forthcoming paragraphs.
After setting the design of the decomposing gate structure, we can override the default number of decomposing layers (i.e. the number describing haw many times a period is repeated in the gate structure) for the decomposition:
In this example we set 60 layers to disentangel the 4-th qubit (i.e. q3) and 16 layers to disentangle the 3-rd qubit (i.e. q2) from the rest.
Finally we start the decomposition by
After the decompsoition is done, we revert the labeling of the qubits to the initial state corresponding to the QX2 architecture:
Using these instructions we revert the labels of the qubits indicated by red numbers to the initial black colored labels. (See figure above showing the "Decomposing gate structure for the QX2 architecture".)
Finally, we show the way to define custom gate structures for the decomposition. First we import and create a class that will hold the design of one period of the decomposing gate structure. (This period of gates is then repeated in the quantum circuit.)
Then we can initialize the label of the qubit we need to disentangle. (SQUANDER always disentagles the qubit with the highes label.)
The custom gate structure can be constructed by the creation of a layers and appending gates into it. The layer is defined again by an instance of class qgd_Gates_block:
In the created layer we can choose between the qubits to play the role of the control and the target qubit on demand. Whatever is our choice, we should apply U3 gates to the qubits in front of the two-qubit controlled gate.
The U3 gates should have two free parameters, lets say variable Theta and Lambda, while parameter Phi is kept constant zero during the decompsition. (Parameters set to True are free parameters, while parameters set to False are kept constant.) In the code snippet above a connection between qubits 0 and 1 is created via a CNOT gate. In particular, qubit 1 is chosen as the target qubit, and qubit 0 is chosen to be the target qubit. Finally, the created layer should be added to the class instance holding the gate design to be used in the decomposiotion
Here we constructed only a single layer, other layers can be constructed following the same logic. The whole, functioning code of the example can be found in example file example_QX2.py.
Solution of the 4th problem of the IBM Challenge 2020
Now we turn our attention to solve the 4th problem of the IBM Challenge 2020. Here we demonstrate that advanced tuning of parameters can help to decompose special unitaries into quantum circuits wirh few CNOT gates. We show haw the SQUANDER package can be used to decompose the unitary of the 4th problem of the IBM Challenge 2020 using 4 CZ gates.
After importing the qgd_python.decomposition.qgd_N_Qubit_Decomposition_adaptive class by command,
we need to load the 4-qubit matrix of the problem from a file shipped with the SQUANDER package:
Then we create the class to be used for the decomposition, which synthesize the given unitary in terms of of CZ, U3 and RX operations:
Notice, that we gave the complex transpose of the unitary Umtx as an input for the class qgd_python.decomposition.qgd_N_Qubit_Decomposition_adaptive. This can be explained by simple linear algebra considerations: since the product of the unitary with it's complex transpose ( \(U U^\dagger=I\)) gives identity, the sequence of operations bringing a unitary \(U\) into identity would naturally equal to the complex transpose \(U^\dagger\) of the unitary \(U\).
Along with the input unitary we provided two other inputs for the decomposition class.
- level_limit_max The maximal number of decomposing unit cells used in the synthesis
- level_limit_min The minimal number of decomposing unit cells used in the synthesis.
Finally, we set the verbosity to the highest level:
and start the decomposition by the command:
The second command in the above code snippet prints the list of decomposing operations on the standard output. Finally, we can export a Qiskit compatible quantum circuit via the SQUANDER Python interface and calculate the final error of the decomposition by the following code snippet:
The documentation of Qiskit, which is needed to fully understand the above code snippet, can be found here.
 1.8.13
1.8.13