LU decomposition of a matrix with partial pivoting, and related features. More...

#include <PartialPivLU.h>

Inheritance diagram for Eigen::PartialPivLU< _MatrixType >:

Public Types
enum	{ MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }

typedef _MatrixType	MatrixType

typedef SolverBase< PartialPivLU >	Base

typedef PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >	PermutationType

typedef Transpositions< RowsAtCompileTime, MaxRowsAtCompileTime >	TranspositionType

typedef MatrixType::PlainObject	PlainObject

Public Types inherited from Eigen::SolverBase< PartialPivLU< _MatrixType > >
enum

typedef EigenBase< PartialPivLU< _MatrixType > >	Base

typedef internal::traits< PartialPivLU< _MatrixType > >::Scalar	Scalar

typedef Scalar	CoeffReturnType

typedef internal::add_const< Transpose< const PartialPivLU< _MatrixType > > >::type	ConstTransposeReturnType

typedef internal::conditional< NumTraits< Scalar >::IsComplex, CwiseUnaryOp< internal::scalar_conjugate_op< Scalar >, ConstTransposeReturnType >, ConstTransposeReturnType >::type	AdjointReturnType

Public Types inherited from Eigen::EigenBase< Derived >
typedef Eigen::Index	Index
	The interface type of indices. More...

typedef internal::traits< Derived >::StorageKind	StorageKind

Public Member Functions
	PartialPivLU ()
	Default Constructor. More...

	PartialPivLU (Index size)
	Default Constructor with memory preallocation. More...

template<typename InputType >
	PartialPivLU (const EigenBase< InputType > &matrix)
	Constructor. More...

template<typename InputType >
	PartialPivLU (EigenBase< InputType > &matrix)
	Constructor for inplace decomposition . More...

template<typename InputType >
PartialPivLU &	compute (const EigenBase< InputType > &matrix)

const MatrixType &	matrixLU () const

const PermutationType &	permutationP () const

template<typename Rhs >
const Solve< PartialPivLU, Rhs >	solve (const MatrixBase< Rhs > &b) const
	This method returns the solution x to the equation Ax=b, where A is the matrix of which *this is the LU decomposition. More...

RealScalar	rcond () const

const Inverse< PartialPivLU >	inverse () const

Scalar	determinant () const

MatrixType	reconstructedMatrix () const

Index	rows () const

Index	cols () const

template<typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl (const RhsType &rhs, DstType &dst) const

template<bool Conjugate, typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl_transposed (const RhsType &rhs, DstType &dst) const

Public Member Functions inherited from Eigen::SolverBase< PartialPivLU< _MatrixType > >
	SolverBase ()
	Default constructor.

const Solve< PartialPivLU< _MatrixType >, Rhs >	solve (const MatrixBase< Rhs > &b) const

ConstTransposeReturnType	transpose () const

AdjointReturnType	adjoint () const

Public Member Functions inherited from Eigen::EigenBase< Derived >
EIGEN_DEVICE_FUNC Derived &	derived ()

EIGEN_DEVICE_FUNC const Derived &	derived () const

EIGEN_DEVICE_FUNC Derived &	const_cast_derived () const

EIGEN_DEVICE_FUNC const Derived &	const_derived () const

EIGEN_DEVICE_FUNC Index	rows () const

EIGEN_DEVICE_FUNC Index	cols () const

EIGEN_DEVICE_FUNC Index	size () const

template<typename Dest >
EIGEN_DEVICE_FUNC void	evalTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	addTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	subTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	applyThisOnTheRight (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	applyThisOnTheLeft (Dest &dst) const

Protected Member Functions
void	compute ()

Static Protected Member Functions
static void	check_template_parameters ()

Protected Attributes
MatrixType	m_lu

PermutationType	m_p

TranspositionType	m_rowsTranspositions

RealScalar	m_l1_norm

signed char	m_det_p

bool	m_isInitialized

Detailed Description

template<typename _MatrixType>
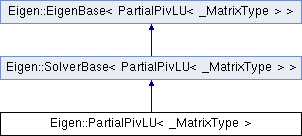
class Eigen::PartialPivLU< _MatrixType >

LU decomposition of a matrix with partial pivoting, and related features.

Template Parameters

_MatrixType the type of the matrix of which we are computing the LU decomposition

This class represents a LU decomposition of a square invertible matrix, with partial pivoting: the matrix A is decomposed as A = PLU where L is unit-lower-triangular, U is upper-triangular, and P is a permutation matrix.

Typically, partial pivoting LU decomposition is only considered numerically stable for square invertible matrices. Thus LAPACK's dgesv and dgesvx require the matrix to be square and invertible. The present class does the same. It will assert that the matrix is square, but it won't (actually it can't) check that the matrix is invertible: it is your task to check that you only use this decomposition on invertible matrices.

The guaranteed safe alternative, working for all matrices, is the full pivoting LU decomposition, provided by class FullPivLU.

This is not a rank-revealing LU decomposition. Many features are intentionally absent from this class, such as rank computation. If you need these features, use class FullPivLU.

This LU decomposition is suitable to invert invertible matrices. It is what MatrixBase::inverse() uses in the general case. On the other hand, it is not suitable to determine whether a given matrix is invertible.

The data of the LU decomposition can be directly accessed through the methods matrixLU(), permutationP().

This class supports the inplace decomposition mechanism.

See also: MatrixBase::partialPivLu(), MatrixBase::determinant(), MatrixBase::inverse(), MatrixBase::computeInverse(), class FullPivLU

Constructor & Destructor Documentation

§ PartialPivLU() [1/4]

template<typename MatrixType >

Eigen::PartialPivLU< MatrixType >::PartialPivLU ( )

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via PartialPivLU::compute(const MatrixType&).

§ PartialPivLU() [2/4]

template<typename MatrixType >

Eigen::PartialPivLU< MatrixType >::PartialPivLU ( Index size )

explicit

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also: PartialPivLU()

§ PartialPivLU() [3/4]

template<typename MatrixType >

template<typename InputType >

Eigen::PartialPivLU< MatrixType >::PartialPivLU ( const EigenBase< InputType > & matrix )

explicit

Constructor.

Parameters

matrix the matrix of which to compute the LU decomposition.

Warning: The matrix should have full rank (e.g. if it's square, it should be invertible). If you need to deal with non-full rank, use class FullPivLU instead.

§ PartialPivLU() [4/4]

template<typename MatrixType >

template<typename InputType >

Eigen::PartialPivLU< MatrixType >::PartialPivLU ( EigenBase< InputType > & matrix )

explicit

Constructor for inplace decomposition .

Parameters

matrix the matrix of which to compute the LU decomposition.

Warning: The matrix should have full rank (e.g. if it's square, it should be invertible). If you need to deal with non-full rank, use class FullPivLU instead.

Member Function Documentation

§ determinant()

template<typename MatrixType >

PartialPivLU< MatrixType >::Scalar Eigen::PartialPivLU< MatrixType >::determinant ( ) const

Returns: the determinant of the matrix of which *this is the LU decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the LU decomposition has already been computed.

Note: For fixed-size matrices of size up to 4, MatrixBase::determinant() offers optimized paths.

Warning: a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow.

See also: MatrixBase::determinant()

§ inverse()

template<typename _MatrixType>

const Inverse<PartialPivLU> Eigen::PartialPivLU< _MatrixType >::inverse ( ) const

inline

Returns: the inverse of the matrix of which *this is the LU decomposition.

Warning: The matrix being decomposed here is assumed to be invertible. If you need to check for invertibility, use class FullPivLU instead.

See also: MatrixBase::inverse(), LU::inverse()

§ matrixLU()

template<typename _MatrixType>

const MatrixType& Eigen::PartialPivLU< _MatrixType >::matrixLU ( ) const

inline

Returns: the LU decomposition matrix: the upper-triangular part is U, the unit-lower-triangular part is L (at least for square matrices; in the non-square case, special care is needed, see the documentation of class FullPivLU).

See also: matrixL(), matrixU()

§ permutationP()

template<typename _MatrixType>

const PermutationType& Eigen::PartialPivLU< _MatrixType >::permutationP ( ) const

inline

Returns: the permutation matrix P.

§ rcond()

template<typename _MatrixType>

RealScalar Eigen::PartialPivLU< _MatrixType >::rcond ( ) const

inline

Returns: an estimate of the reciprocal condition number of the matrix of which *this is the LU decomposition.

§ reconstructedMatrix()

template<typename MatrixType >

MatrixType Eigen::PartialPivLU< MatrixType >::reconstructedMatrix ( ) const

Returns: the matrix represented by the decomposition, i.e., it returns the product: P^{-1} L U. This function is provided for debug purpose.

§ solve()

template<typename _MatrixType>

template<typename Rhs >

const Solve<PartialPivLU, Rhs> Eigen::PartialPivLU< _MatrixType >::solve ( const MatrixBase< Rhs > & b ) const

inline

This method returns the solution x to the equation Ax=b, where A is the matrix of which *this is the LU decomposition.

Parameters

b	the right-hand-side of the equation to solve. Can be a vector or a matrix, the only requirement in order for the equation to make sense is that b.rows()==A.rows(), where A is the matrix of which *this is the LU decomposition.

Returns: the solution.

Example:

Output:

Since this PartialPivLU class assumes anyway that the matrix A is invertible, the solution theoretically exists and is unique regardless of b.

See also: TriangularView::solve(), inverse(), computeInverse()

The documentation for this class was generated from the following files:

third-party-libs/eigen3/Eigen/src/Core/util/ForwardDeclarations.h
third-party-libs/eigen3/Eigen/src/LU/PartialPivLU.h

Public Types

Public Member Functions

Protected Member Functions

Static Protected Member Functions

Protected Attributes

Detailed Description

template<typename _MatrixType> class Eigen::PartialPivLU< _MatrixType >

Constructor & Destructor Documentation

§ PartialPivLU() [1/4]

§ PartialPivLU() [2/4]

§ PartialPivLU() [3/4]

§ PartialPivLU() [4/4]

Member Function Documentation

§ determinant()

§ inverse()

§ matrixLU()

§ permutationP()

§ rcond()

§ reconstructedMatrix()

§ solve()

template<typename _MatrixType>
class Eigen::PartialPivLU< _MatrixType >