Expression of a selfadjoint matrix from a triangular part of a dense matrix. More...

#include <SelfAdjointView.h>

Inheritance diagram for Eigen::SelfAdjointView< _MatrixType, UpLo >:

Public Types
enum	{ Mode = internal::traits<SelfAdjointView>::Mode, Flags = internal::traits<SelfAdjointView>::Flags }

typedef _MatrixType	MatrixType

typedef TriangularBase< SelfAdjointView >	Base

typedef internal::traits< SelfAdjointView >::MatrixTypeNested	MatrixTypeNested

typedef internal::traits< SelfAdjointView >::MatrixTypeNestedCleaned	MatrixTypeNestedCleaned

typedef MatrixTypeNestedCleaned	NestedExpression

typedef internal::traits< SelfAdjointView >::Scalar	Scalar
	The type of coefficients in this matrix.

typedef MatrixType::StorageIndex	StorageIndex

typedef MatrixType::PlainObject	PlainObject

typedef NumTraits< Scalar >::Real	RealScalar
	Real part of Scalar.

typedef Matrix< RealScalar, internal::traits< MatrixType >::ColsAtCompileTime, 1 >	EigenvaluesReturnType
	Return type of eigenvalues()

Public Types inherited from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >
enum

typedef internal::traits< SelfAdjointView< _MatrixType, UpLo > >::Scalar	Scalar

typedef internal::traits< SelfAdjointView< _MatrixType, UpLo > >::StorageKind	StorageKind

typedef internal::traits< SelfAdjointView< _MatrixType, UpLo > >::StorageIndex	StorageIndex

typedef internal::traits< SelfAdjointView< _MatrixType, UpLo > >::FullMatrixType	DenseMatrixType

typedef DenseMatrixType	DenseType

typedef SelfAdjointView< _MatrixType, UpLo > const &	Nested

Public Types inherited from Eigen::EigenBase< Derived >
typedef Eigen::Index	Index
	The interface type of indices. More...

typedef internal::traits< Derived >::StorageKind	StorageKind

Public Member Functions
EIGEN_DEVICE_FUNC	SelfAdjointView (MatrixType &matrix)

EIGEN_DEVICE_FUNC Index	rows () const

EIGEN_DEVICE_FUNC Index	cols () const

EIGEN_DEVICE_FUNC Index	outerStride () const

EIGEN_DEVICE_FUNC Index	innerStride () const

EIGEN_DEVICE_FUNC Scalar	coeff (Index row, Index col) const

EIGEN_DEVICE_FUNC Scalar &	coeffRef (Index row, Index col)

EIGEN_DEVICE_FUNC const MatrixTypeNestedCleaned &	_expression () const

EIGEN_DEVICE_FUNC const MatrixTypeNestedCleaned &	nestedExpression () const

EIGEN_DEVICE_FUNC MatrixTypeNestedCleaned &	nestedExpression ()

template<typename OtherDerived >
EIGEN_DEVICE_FUNC const Product< SelfAdjointView, OtherDerived >	operator* (const MatrixBase< OtherDerived > &rhs) const
	Efficient triangular matrix times vector/matrix product.

template<typename DerivedU , typename DerivedV >
EIGEN_DEVICE_FUNC SelfAdjointView &	rankUpdate (const MatrixBase< DerivedU > &u, const MatrixBase< DerivedV > &v, const Scalar &alpha=Scalar(1))
	Perform a symmetric rank 2 update of the selfadjoint matrix `this`: \( this = this + \alpha u v^ + conj(\alpha) v u^* \). More...

template<typename DerivedU >
EIGEN_DEVICE_FUNC SelfAdjointView &	rankUpdate (const MatrixBase< DerivedU > &u, const Scalar &alpha=Scalar(1))
	Perform a symmetric rank K update of the selfadjoint matrix `this`: \( this = this + \alpha ( u u^ ) \) where u is a vector or matrix. More...

template<unsigned int TriMode>
EIGEN_DEVICE_FUNC internal::conditional<(TriMode &(Upper\|Lower))==(UpLo &(Upper\|Lower)), TriangularView< MatrixType, TriMode >, TriangularView< typename MatrixType::AdjointReturnType, TriMode > >::type	triangularView () const

EIGEN_DEVICE_FUNC MatrixType::ConstDiagonalReturnType	diagonal () const

const LLT< PlainObject, UpLo >	llt () const

const LDLT< PlainObject, UpLo >	ldlt () const

EIGEN_DEVICE_FUNC EigenvaluesReturnType	eigenvalues () const
	Computes the eigenvalues of a matrix. More...

EIGEN_DEVICE_FUNC RealScalar	operatorNorm () const
	Computes the L2 operator norm. More...

template<typename DerivedU >
SelfAdjointView< MatrixType, UpLo > &	rankUpdate (const MatrixBase< DerivedU > &u, const Scalar &alpha)

template<typename DerivedU , typename DerivedV >
SelfAdjointView< MatrixType, UpLo > &	rankUpdate (const MatrixBase< DerivedU > &u, const MatrixBase< DerivedV > &v, const Scalar &alpha)

Public Member Functions inherited from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >
EIGEN_DEVICE_FUNC Index	rows () const

EIGEN_DEVICE_FUNC Index	cols () const

EIGEN_DEVICE_FUNC Index	outerStride () const

EIGEN_DEVICE_FUNC Index	innerStride () const

void	resize (Index rows, Index cols)

EIGEN_DEVICE_FUNC Scalar	coeff (Index row, Index col) const

EIGEN_DEVICE_FUNC Scalar &	coeffRef (Index row, Index col)

EIGEN_DEVICE_FUNC EIGEN_STRONG_INLINE void	copyCoeff (Index row, Index col, Other &other)

EIGEN_DEVICE_FUNC Scalar	operator() (Index row, Index col) const

EIGEN_DEVICE_FUNC Scalar &	operator() (Index row, Index col)

EIGEN_DEVICE_FUNC const SelfAdjointView< _MatrixType, UpLo > &	derived () const

EIGEN_DEVICE_FUNC SelfAdjointView< _MatrixType, UpLo > &	derived ()

EIGEN_DEVICE_FUNC void	evalTo (MatrixBase< DenseDerived > &other) const

void	evalTo (MatrixBase< DenseDerived > &other) const
	Assigns a triangular or selfadjoint matrix to a dense matrix. More...

EIGEN_DEVICE_FUNC void	evalToLazy (MatrixBase< DenseDerived > &other) const

void	evalToLazy (MatrixBase< DenseDerived > &other) const
	Assigns a triangular or selfadjoint matrix to a dense matrix. More...

EIGEN_DEVICE_FUNC DenseMatrixType	toDenseMatrix () const

Public Member Functions inherited from Eigen::EigenBase< Derived >
EIGEN_DEVICE_FUNC Derived &	derived ()

EIGEN_DEVICE_FUNC const Derived &	derived () const

EIGEN_DEVICE_FUNC Derived &	const_cast_derived () const

EIGEN_DEVICE_FUNC const Derived &	const_derived () const

EIGEN_DEVICE_FUNC Index	rows () const

EIGEN_DEVICE_FUNC Index	cols () const

EIGEN_DEVICE_FUNC Index	size () const

template<typename Dest >
EIGEN_DEVICE_FUNC void	evalTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	addTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	subTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	applyThisOnTheRight (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	applyThisOnTheLeft (Dest &dst) const

Protected Attributes
MatrixTypeNested	m_matrix

Friends
template<typename OtherDerived >
EIGEN_DEVICE_FUNC const Product< OtherDerived, SelfAdjointView >	operator* (const MatrixBase< OtherDerived > &lhs, const SelfAdjointView &rhs)
	Efficient vector/matrix times triangular matrix product.

EIGEN_DEVICE_FUNC const SelfAdjointView< const EIGEN_SCALAR_BINARYOP_EXPR_RETURN_TYPE(Scalar, MatrixType, product), UpLo >	operator* (const Scalar &s, const SelfAdjointView &mat)

Additional Inherited Members
Protected Member Functions inherited from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >
void	check_coordinates (Index row, Index col) const

void	check_coordinates_internal (Index, Index) const

Detailed Description

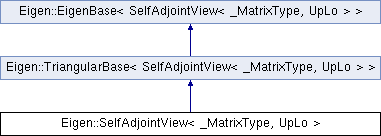
template<typename _MatrixType, unsigned int UpLo>
class Eigen::SelfAdjointView< _MatrixType, UpLo >

Expression of a selfadjoint matrix from a triangular part of a dense matrix.

Parameters

MatrixType	the type of the dense matrix storing the coefficients
TriangularPart	can be either `Lower` or `Upper`

This class is an expression of a sefladjoint matrix from a triangular part of a matrix with given dense storage of the coefficients. It is the return type of MatrixBase::selfadjointView() and most of the time this is the only way that it is used.

See also: class TriangularBase, MatrixBase::selfadjointView()

Member Function Documentation

§ coeff()

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Scalar Eigen::SelfAdjointView< _MatrixType, UpLo >::coeff	(	Index	row,
		Index	col
	)		const

inline

See also: MatrixBase::coeff()

Warning: the coordinates must fit into the referenced triangular part

§ coeffRef()

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Scalar& Eigen::SelfAdjointView< _MatrixType, UpLo >::coeffRef	(	Index	row,
		Index	col
	)

inline

See also: MatrixBase::coeffRef()

Warning: the coordinates must fit into the referenced triangular part

§ diagonal()

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC MatrixType::ConstDiagonalReturnType Eigen::SelfAdjointView< _MatrixType, UpLo >::diagonal ( ) const

inline

Returns: a const expression of the main diagonal of the matrix *this

This method simply returns the diagonal of the nested expression, thus by-passing the SelfAdjointView decorator.

See also: MatrixBase::diagonal(), class Diagonal

§ eigenvalues()

template<typename MatrixType , unsigned int UpLo>

SelfAdjointView< MatrixType, UpLo >::EigenvaluesReturnType Eigen::SelfAdjointView< MatrixType, UpLo >::eigenvalues ( ) const

inline

Computes the eigenvalues of a matrix.

Returns: Column vector containing the eigenvalues.

This function computes the eigenvalues with the help of the SelfAdjointEigenSolver class. The eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix.

Example:

Output:

See also: SelfAdjointEigenSolver::eigenvalues(), MatrixBase::eigenvalues()

§ ldlt()

template<typename MatrixType , unsigned int UpLo>

const LDLT< typename SelfAdjointView< MatrixType, UpLo >::PlainObject, UpLo > Eigen::SelfAdjointView< MatrixType, UpLo >::ldlt ( ) const

inline

Returns: the Cholesky decomposition with full pivoting without square root of *this

See also: MatrixBase::ldlt()

§ llt()

template<typename MatrixType , unsigned int UpLo>

const LLT< typename SelfAdjointView< MatrixType, UpLo >::PlainObject, UpLo > Eigen::SelfAdjointView< MatrixType, UpLo >::llt ( ) const

inline

Returns: the LLT decomposition of *this

See also: SelfAdjointView::llt()

§ operatorNorm()

template<typename MatrixType , unsigned int UpLo>

SelfAdjointView< MatrixType, UpLo >::RealScalar Eigen::SelfAdjointView< MatrixType, UpLo >::operatorNorm ( ) const

inline

Computes the L2 operator norm.

Returns: Operator norm of the matrix.

This function computes the L2 operator norm of a self-adjoint matrix. For a self-adjoint matrix, the operator norm is the largest eigenvalue.

The current implementation uses the eigenvalues of the matrix, as computed by eigenvalues(), to compute the operator norm of the matrix.

Example:

Output:

See also: eigenvalues(), MatrixBase::operatorNorm()

§ rankUpdate() [1/2]

template<typename _MatrixType, unsigned int UpLo>

template<typename DerivedU , typename DerivedV >

EIGEN_DEVICE_FUNC SelfAdjointView& Eigen::SelfAdjointView< _MatrixType, UpLo >::rankUpdate	(	const MatrixBase< DerivedU > &	u,
		const MatrixBase< DerivedV > &	v,
		const Scalar &	alpha = `Scalar(1)`
	)

Perform a symmetric rank 2 update of the selfadjoint matrix *this: \( this = this + \alpha u v^* + conj(\alpha) v u^* \).

Returns: a reference to *this

The vectors u and v must be column vectors, however they can be a adjoint expression without any overhead. Only the meaningful triangular part of the matrix is updated, the rest is left unchanged.

See also: rankUpdate(const MatrixBase<DerivedU>&, Scalar)

§ rankUpdate() [2/2]

template<typename _MatrixType, unsigned int UpLo>

template<typename DerivedU >

EIGEN_DEVICE_FUNC SelfAdjointView& Eigen::SelfAdjointView< _MatrixType, UpLo >::rankUpdate	(	const MatrixBase< DerivedU > &	u,
		const Scalar &	alpha = `Scalar(1)`
	)

Perform a symmetric rank K update of the selfadjoint matrix *this: \( this = this + \alpha ( u u^* ) \) where u is a vector or matrix.

Returns: a reference to *this

Note that to perform \( this = this + \alpha ( u^* u ) \) you can simply call this function with u.adjoint().

See also: rankUpdate(const MatrixBase<DerivedU>&, const MatrixBase<DerivedV>&, Scalar)

§ triangularView()

template<typename _MatrixType, unsigned int UpLo>

template<unsigned int TriMode>

EIGEN_DEVICE_FUNC internal::conditional<(TriMode&(Upper|Lower))==(UpLo&(Upper|Lower)), TriangularView<MatrixType,TriMode>, TriangularView<typename MatrixType::AdjointReturnType,TriMode> >::type Eigen::SelfAdjointView< _MatrixType, UpLo >::triangularView ( ) const

inline

Returns: an expression of a triangular view extracted from the current selfadjoint view of a given triangular part

The parameter TriMode can have the following values: Upper, StrictlyUpper, UnitUpper, Lower, StrictlyLower, UnitLower.

If TriMode references the same triangular part than *this, then this method simply return a TriangularView of the nested expression, otherwise, the nested expression is first transposed, thus returning a TriangularView<Transpose<MatrixType>> object.

See also: MatrixBase::triangularView(), class TriangularView

The documentation for this class was generated from the following files:

third-party-libs/eigen3/Eigen/src/Core/SelfAdjointView.h
third-party-libs/eigen3/Eigen/src/Cholesky/LDLT.h
third-party-libs/eigen3/Eigen/src/Cholesky/LLT.h
third-party-libs/eigen3/Eigen/src/Core/products/SelfadjointProduct.h
third-party-libs/eigen3/Eigen/src/Core/products/SelfadjointRank2Update.h
third-party-libs/eigen3/Eigen/src/Eigenvalues/MatrixBaseEigenvalues.h

Public Types

Public Member Functions

Protected Attributes

Friends

Additional Inherited Members

Detailed Description

template<typename _MatrixType, unsigned int UpLo> class Eigen::SelfAdjointView< _MatrixType, UpLo >

Member Function Documentation

§ coeff()

§ coeffRef()

§ diagonal()

§ eigenvalues()

§ ldlt()

§ llt()

§ operatorNorm()

§ rankUpdate() [1/2]

§ rankUpdate() [2/2]

§ triangularView()

template<typename _MatrixType, unsigned int UpLo>
class Eigen::SelfAdjointView< _MatrixType, UpLo >